Software Defined Radiofrequency signal processing (SDR) – GNURadio
 
J.-M Friedt,

First steps with GNURadio

GNURadio provides a set of digital signal processing blocks as well as a scheduler taking care of data flow. Signal processing blocks are written in C++ or in Python. Assembling blocks as a processing chain is defined by a Python script. A graphical user interface is not mandatory, making GNURadio well suited for embedded environments not fitted with graphical displays (e.g. Redpitaya board).

A tool helps in assembling blocks – which actually happens to be a Python code generator from the processing chain graphically defined – named GNURadio Companion. We shall use this tool, called gnuradio-companion from the command line interface, for this introduction to software defined radio (SDR) digital signal processing.

Sound card output

We can test basic – yet fundamental – signal processing algorithms such as filters. A Finite Impulse Filter (FIR) is designed to process synthetic data. In order to characterize the spectral characteristics of the filter, we feed it with a white noise source, and observe the spectrum at the input and the output of the filter.

In order to become familiar with GNURadio-companion, a first example aims at generating a processing flow fed by a noise source, a band-pass filter of varying central frequency and bandpass, and a display of the resulting spectrum (Fig. 1)

In this example, the data sink is a sound card. The sampling rate along the whole flowgraph is defined with the variable samp_rate which must be set to one of the sampling rates supported by the hardware, in this case 96 kHz. Making sure the sampling rate is consistent along the processing chain must be taken care of by the designer and will not be handled by GNU Radio: most specifically, interpolation will increase the sampling rate and decimation will reduce the sampling rate. In this example, decimation is set to 1 and there is no interpolation, so the sampling rate remains constant throughout the flowchart.

1. Find, on the GNURadio website, the API describing the signal processing blocks, and the methods associated to the “band pass filter” object.

2. Add to the Python script generated by GNURadio-companion an output printing the length of the filter.

3. Output the processed signal on the sound card: listen at the impact of the bandwidth and central frequency of the filter.

How to handle data-flow when lacking input or output hardware

When the signal is emitted by the sound card, the data-rate is defined by the sampling rate of the sound card. If a signal is sampled from an acquisition card, here again the sampling rate is defined. But if we only perform signal processing on synthetic data or data stored in a file to display its characteristics, no sampling rate is imposed in the processing flowchart by a hardware interface. We must tell the scheduler to wait between two processing steps to comply with the expected sampling rate defined by the samp_rate variable: the throttle bloc is in charge of such an operation.

1. Remove the audio output and display on a virtual oscilloscope the output of the filtered output.

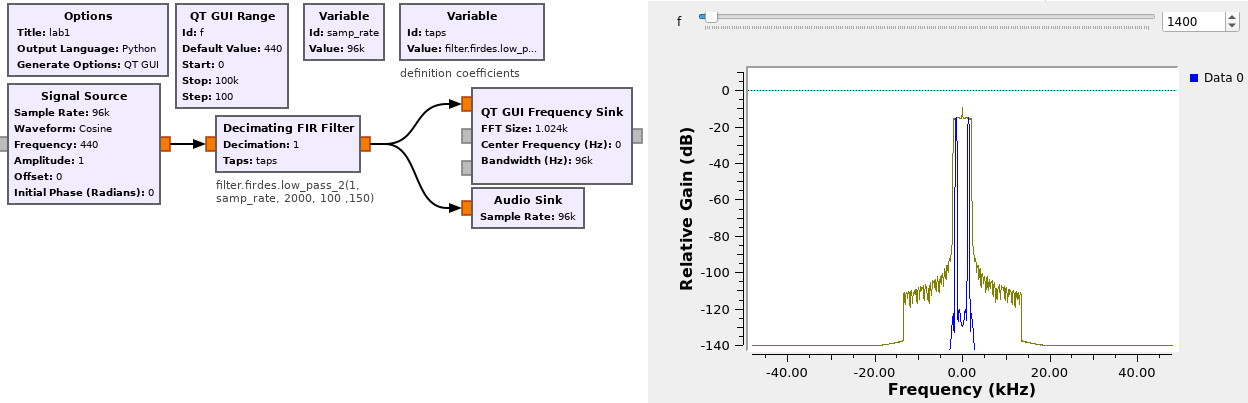
Let us demonstrate the flexibility of GNURadio-companion to address and prototype signal processing concepts by printing the filter coefficients. A FIR (Finite Impulse Response) filter generates an output $y_n$ as weighted combination of past inputs $x_k$ following $$y_n=\sum_0^N b_k\cdot x_{n-k}$$ with $N$ the number of coefficients. This number significantly impacts the computational processing power needed to generate each $y_n$ and it is important to get a feeling of such an impact. Starting with the processing scheme such as seen on Fig. 2

in which the $b_k$ coefficients, called taps, are dynamically defined by the Python Python
filter.firdes.low_pass_2(1, samp_rate, fc, df ,attenuation)
we define a filter with cutoff frequency fc, a transition width of df and an out of band attenuation of attenuation. We will see that df is a core parameter defining $N$. To get a feeling of the meaning of $N$ and its relation to fc, let us consider how a Fourier transform on $N$ samples will generate a spectrum with frequency steps $samp\_rate/N$, with $samp\_rate$ the sampling rate. If fc is smaller than $samp\_rate/N$, the spectrum is not defined well enough to define the slopes of the filter: $N$ must be increased.

1. Observe how the number of coefficients evolves as a function of the center frequency fc ... or of the transition width df.

GNURadio for practical signal processing

The sound card as a low frequency signal generator

The sound card is an ideally suited interface to become familiar with core concepts of signal processing. GNURadio can emit a signal through the sound card thanks to the Audio Sink block.

1. Generate a sine wave at a frequency that can be heard, and send it to the sound card. Display at the same time the spectrum of the emitted signal.

2. Sweep the sine wave frequency and observe the impact of a low-pass filter on the signal output by display both the original and filtered signal in the time and frequency domains.

Decimation is a core aspect of digital signal processing: the lower the datarate, the fewer processing power is needed so that the sampling rate should be lowered along the processing chain as more and more information is discarded by each processing block. When decimating by a factor D, the output sampling rate is the input sampling rate divided by D. Care must be taken when decimating that the output frequency does not lie above half the new Nyquist frequency (half the decimated sampling frequency) or aliasing will occur (Fig. 3).

1. What happens if the output frequency f is changed from 440 Hz to 95560 Hz in Fig. 3 ?

I-Q coefficients

Processing complex signals is a natural representation of the frequency transposition output of the receiver. When frequency-shifting from the radiofrequency band $A\cos(\omega t+\varphi)$ to baseband (centered around 0 Hz), a single mixer with the local oscillator $\cos(\omega t)$ yields after low-pass filtering the $2\omega$ component the term $A\cos(\varphi)$ which might be always null if $\varphi=\pi/2$, whatever the amplitude modulation $A$. Hence the I/Q demodulator in which a second mixer is used for mixing the incoming radiofrequency signal with a quadrature shifted copy of the local oscillator yielding $A\sin(\varphi)$. These two outputs are conviently expressed as $I+jQ=A\exp(j\varphi)$ with $j^2=-1$. We show here how I/Q coefficients are natural outputs of SDR receivers.

In the following example we feed the function generator with a signal at various frequencies as the DVB-T dongle is set at a fixed frequency of 434 MHz. The complex output of the I/Q demodulator is observed in the time domain: left the input signal is at 433.98 MHz, middle at 433.99 and right at 434 MHz. The imaginary part is observed to be either late, in sync close to the carrier or early: as opposed to the mixing with a real signal which generates both sidebands on the left and right of the carrier frequency, mixing in the complex domain only generates one sideband at the radiofrequency minus the local oscillator frequencies.

Receiving radiofrequency signals: commercial FM broadcast

Displaying the spectrum

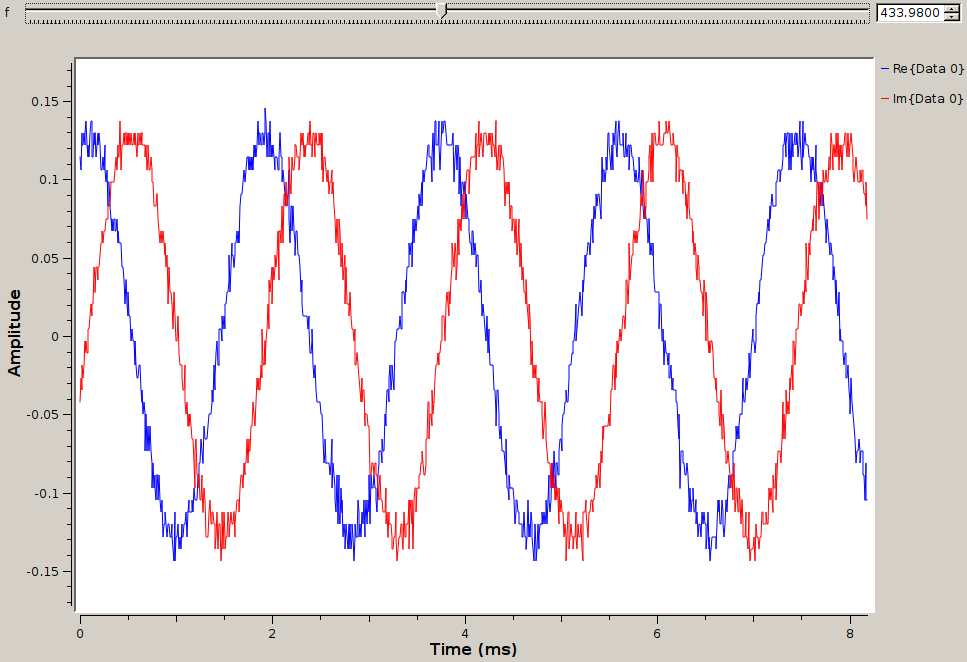
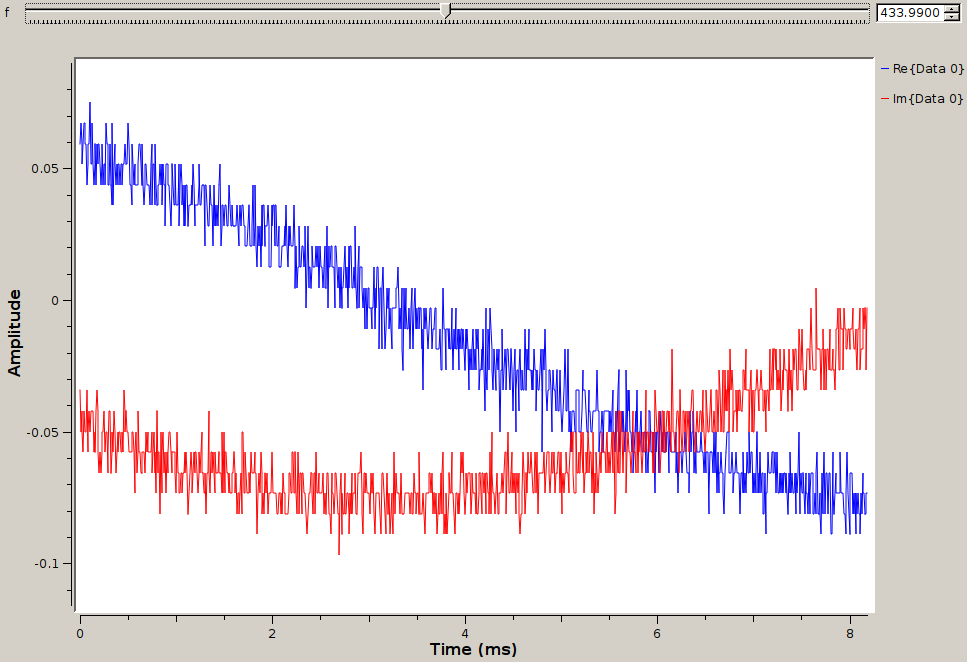
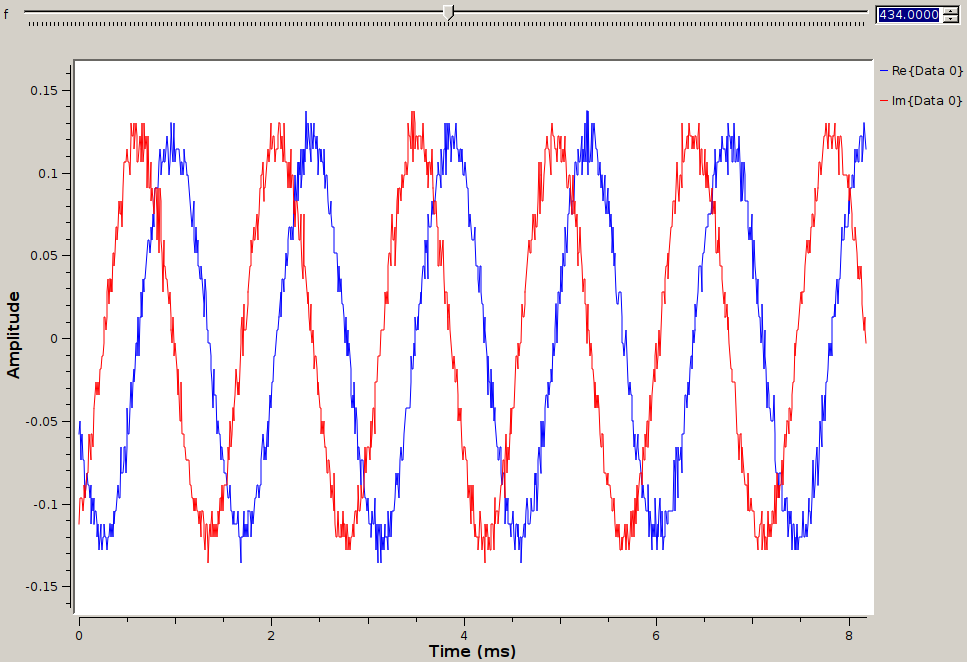
The easiest yet most attractive demonstration of radiofrequency reception is to analyze a commercial FM broadcast station signal and send the audio output to the sound card (Fig. 4). This example is most simple since the received signal is powerful and broadcast continuously, but nevertheless demonstrates the core concepts of SDR. The objectives of this first experiment are

• to become familiar with searching processing blocks in the right menu containing the list of signal processing functions available,

• select the datastream generated by the DVB-T receiver which will be used throughout these labs,

• make sure we understand the consistency of data-flow as decimations are applied at various stages of the processing.

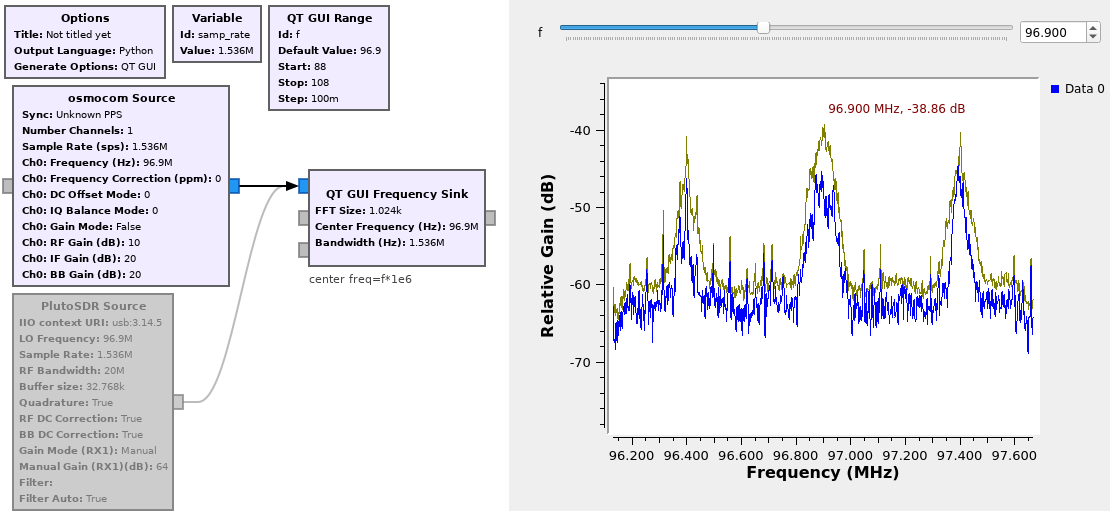
A source provides a complex I and Q data stream to feed the various processing blocks to finally reach a sink – in our case the sound card. The data-rate from the source defines the analysis bandwidth and hence the amount of information we can collect (cf Shannon). The bandwidth is limited by the sampling rate and the communication bandwidth between the acquisition peripheral and the personal computer (in our case, USB bus).

The central working frequency is of hardly any importance – it only defines the antenna size – since the radiofrequency receiver aims at cancelling the carrier with the initial mixing stage. Only the bandwidth matters !

An easily accessible data source is the sound card input (microphone) of a personal computer. The bandwidth is usually limited to 48 or 96 kHz, sometimes 192 kHz depending on the sound card brand. Historically, the output of radiofrequency receivers were connected to the audio-frequency inputs for further digital signal processing (e.g. ACARS or AX25 receivers). In our approach, a low cost digital video broadcast terrestrial (DVB-T) receiver happens to be usable as a general purpose radiofrequency receiver operating in the 50 to 1600 MHz range. Most significantly, it covers the commercial FM broadcast band ranging from 88 to 108 MHz in Europe, or 76 to 95 MHz in Japan.

1. Considering the commercial FM band, what are the associated wavelength and hence antenna dimensions best suited to receive such signal ?

2. What is the typical bandwidth of a broadcast wideband FM communication channel. What low-pass filter width is best selected to prevent adjacent channels from being received while still collecting the whole information from the targeted channel ?

In order to design the FM-receiver:

• Find the source by hitting on the magnifying glass icon osmo which allows isolating the Osmocom Source bloc.

• Find the sink by hitting on the magnifying glass icon QT which allows accessing the QT Frequency Sink.

• Modify the sampling rate variable samp_rate with a value ranging from 1 to 2 MHz.

1. Vary the sampling rate and observe the consequence.

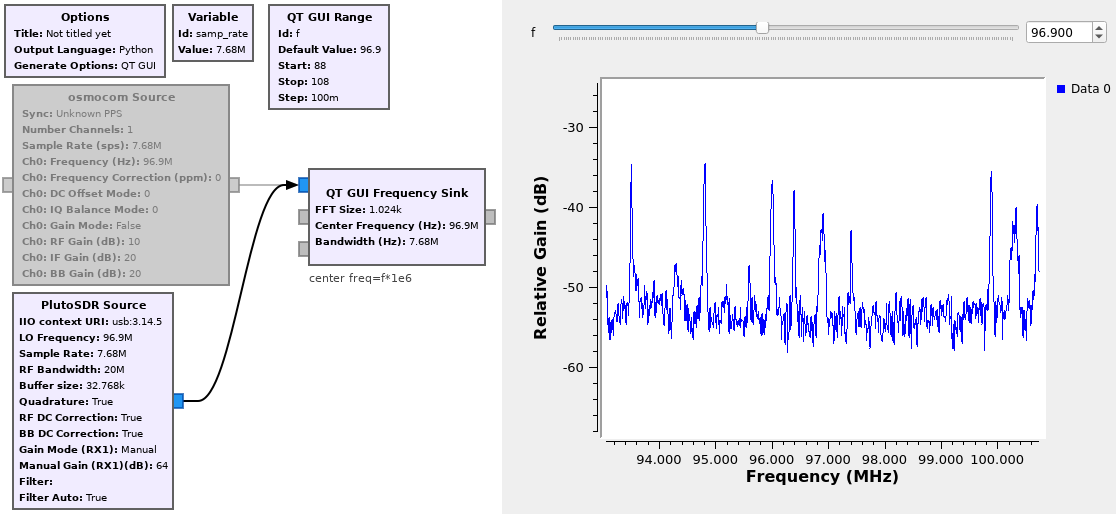
Rather than setting the central operating frequency when starting the acquisition, we might want to dynamically update such a parameter (Fig. 5).

• Create a slider defining the variable $f$ thanks to a QT Range

• Define the central frequency of the receiver with the variable $f$ defining the carrier frequency of the DVB-T receiver

• Define the central frequency of the FFT as being equal to $f$ rather than 0.

Demodulation and audio output

Once the frequency band including the FM broadcast signal has been identified, we must demodulate the signal (extract the information content from the carrier) and send the result to a meaningful peripheral, for example the PC sound card.

The challenges lies in handling the data-flow, which must start with a radiofrequency rate (several hundreds of ksamples/s) to an audio-frequency rate (a few ksamples/s). GNURadio does not automatically handle data flow rates, and only warns the user of an inconsistent data rate with cryptic messages at first sight (but consistent once their meaning has been understood).

The data-rate output from the DVB-T must lie in the 1 to 2,4 Msamples/s (the upper limit being given by the bandwidth of the USB communication link, the lower limit by hardware limitations). The sound card sampling rate must be selected amongst a few possible values such as 48000, 44100, 22150 or, for the older sound cards, 11025 Hz. Handling the data rate requires consistently decimating the data-rate from an initial value to a final value. In order to make sure that the initial sampling rate can easily be decimated to the output audio frequency, it is safe to define samp_rate as a multiple of the output audio frequency. For example for a 48 kHz output sampling rate, an input of $48\times 32=1.536$ MHz complies with the DVB-T receiver sampling rate range. Similarly for a 44,1 kHz output, an input at $44.1\times 50=2.205$ MHz complies with the requirements of the sampling rate of the input and output, assuming the various processing blocks decimate by a factor of $50=5\times 5\times 2$.

1. Connect a headset to the audio output of the PC and listen to the result. What happens if the decimation factor is incorrectly set, for example by selecting a value below 32  above 32 ?

Stereo sound and RDS

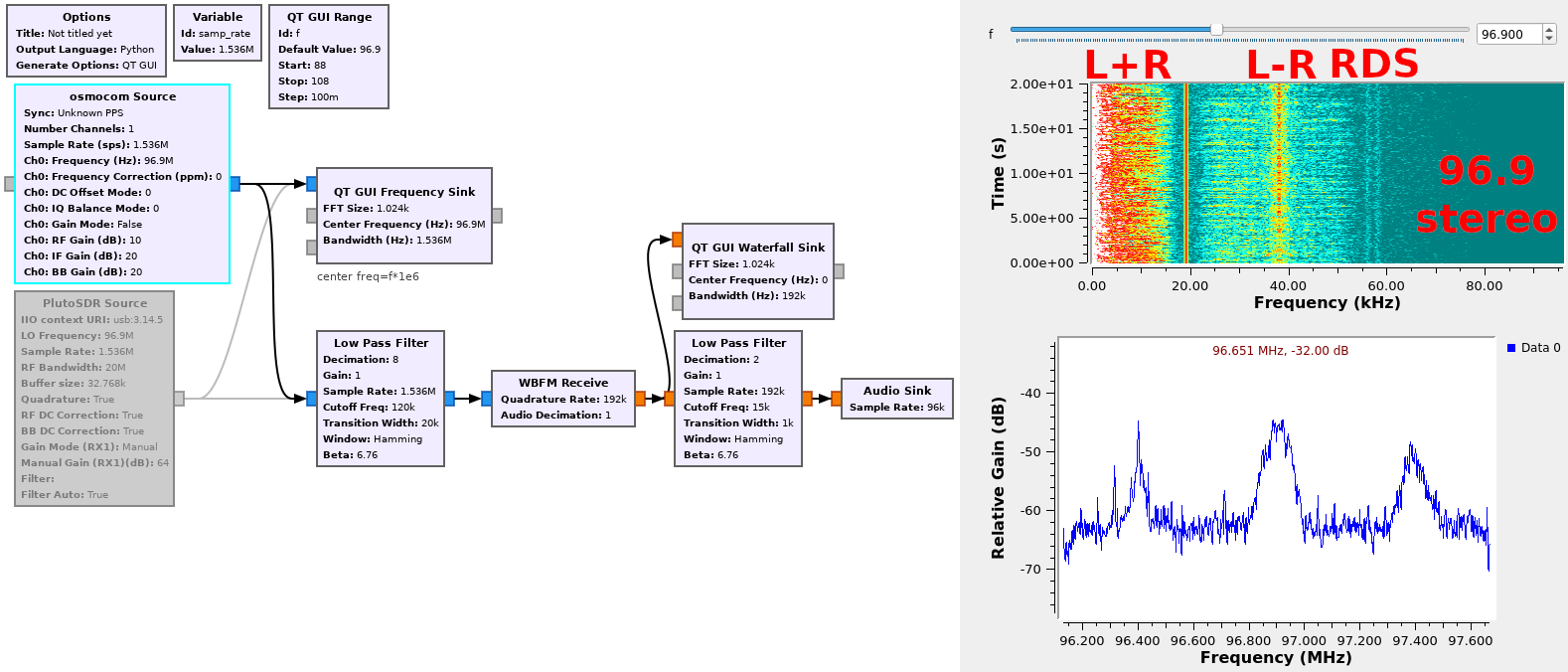
Many FM broadcast stations emit a stereo signal. However, not all receivers are fitted to process separate left ear and right ear signals. What solution can suit both mono and stereo receivers ? The solution consists in transmitting for all receivers the sum of left + right ear sounds, and only for stereo receivers the signal difference left - right so that both separate signals can be reconstructed from the initial information if needed. Furthermore, some radio stations outside Japan emit a digital information defining the kind of program being broadcast and the name of the station: this protocol is named Radio Data System (RDS), located at a frequency offset of 57 kHz, beyond all audio-frequency signal modulations. The bitrate of the digital information, 1187.5 bits/second, is slow enough so as only to use a reduced bandwidth around the 57 kHz sub-carrier generated as the third harmonic of the 19 kHz pilot tone which tells the receiver that the emission is in stereo (and hence that the upper part of the spectrum carries the left-right information).

1. Using the waterfall sink, display the various sub-bands transmitted by the FM broadcast emitter after demodulation (Fig. 6).

Spectral occupation of the various modulation schemes

AM v.s FM

The bandwidth of a communication channel defines the amount of information that can be transmitted. The modulation scheme induces a spectral occupation and hence the distribution of the spectral components within the allocated bandwidth. Fig. 8 illustrates the spectral occupation of two common modulation schemes – AM and FM – to encode the same input signal – a sine wave of fixed frequency and amplitude.

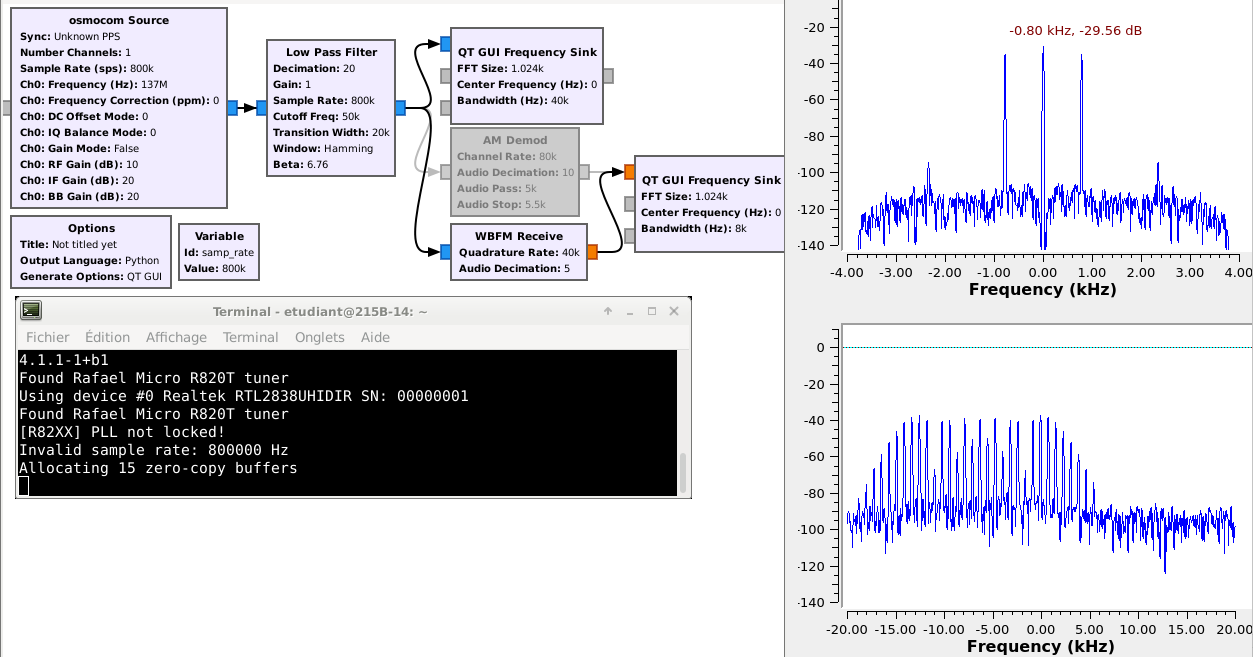
An amplitude modulation is generated by a voltage controlled attenuation, also known as a transistor (for example a FET). A frequency modulation is generated by a voltage controlled oscillator and pulling the frequency as a function of the voltage representing the information to be transmitted (e.g. using a varicap) – (VCO – Voltage Controlled Oscillator).

1. Demodulate the AM and FM signals in order to display the time evolution of the modulated information.

BPSK

Phase modulation is achieved by feeding a mixer (in our case a Minicircuits ZX05-43MH+, Fig. 11) on one side by a radiofrequency carrier signal (LO port) and on the other hand by a square-wave signal with mean value 0 representing the signal (IF port) to generate the signal sent to the antenna (RF port). Based on the internal schematic of the mixer, the polarity of the modulating signal defines the side of the diode bridge through which the LO signal goes to reach the middle point of the transformer, and hence the phase (between $0$ and $\pi$) imprinted on the output signal.

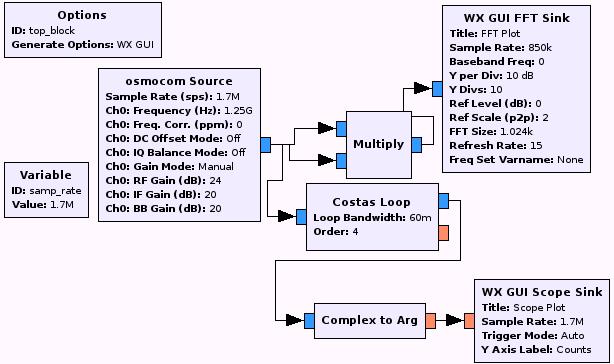
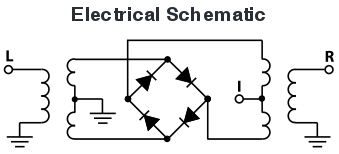
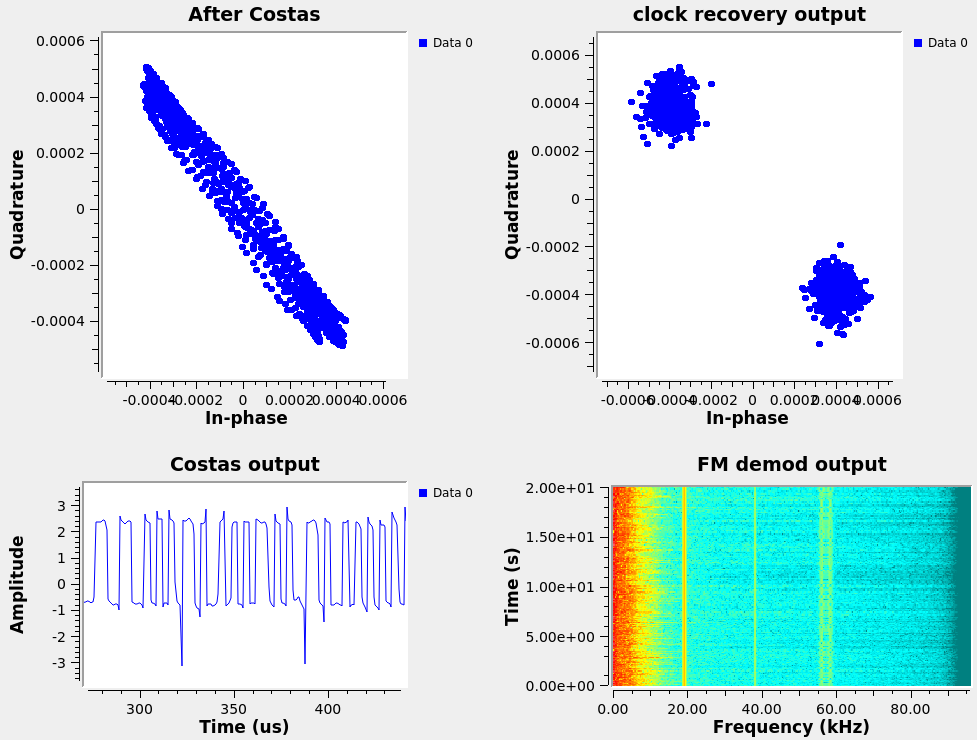
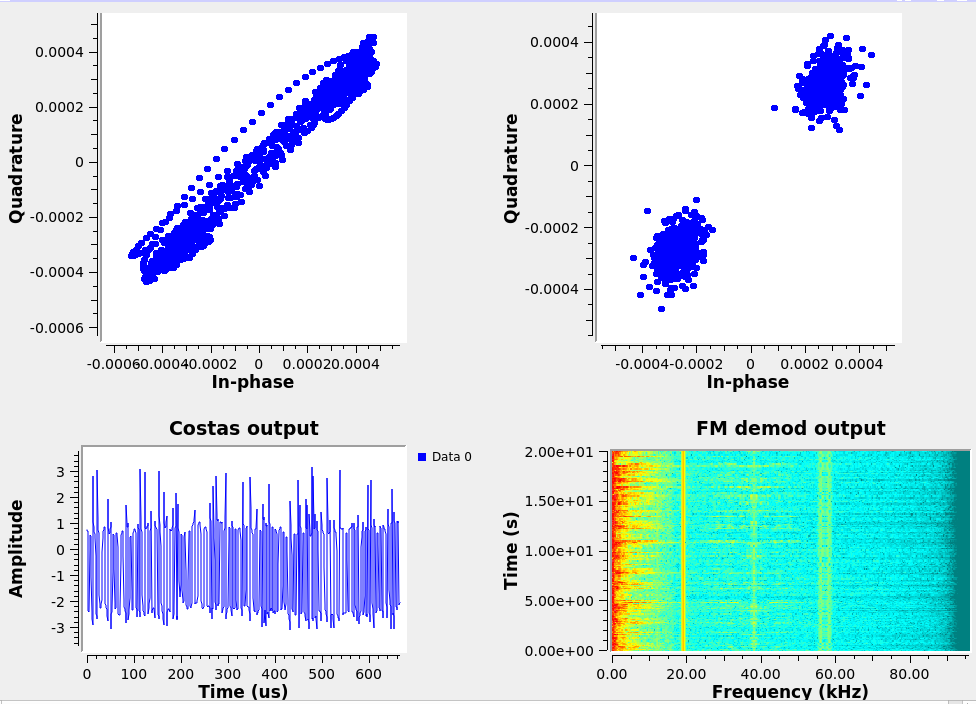
The challenge of PSK demodulation lies in the recovery of the carrier in order to eliminate the frequency offset $\Delta f$ between the local oscillator and the incoming signal. Indeed, were this frequency difference not cancelled, the phase of the signal is on the one hand defined with a continuously changing contribution as a function of time $2\pi\cdot \Delta f\cdot t$ and on the other hand with the phase to be detected $\varphi\in[0,\pi]$. One way of estimating the carrier frequency offset is by using the Costas loop which provides the demodulated signal in addition to an indicator of the frequency offset.

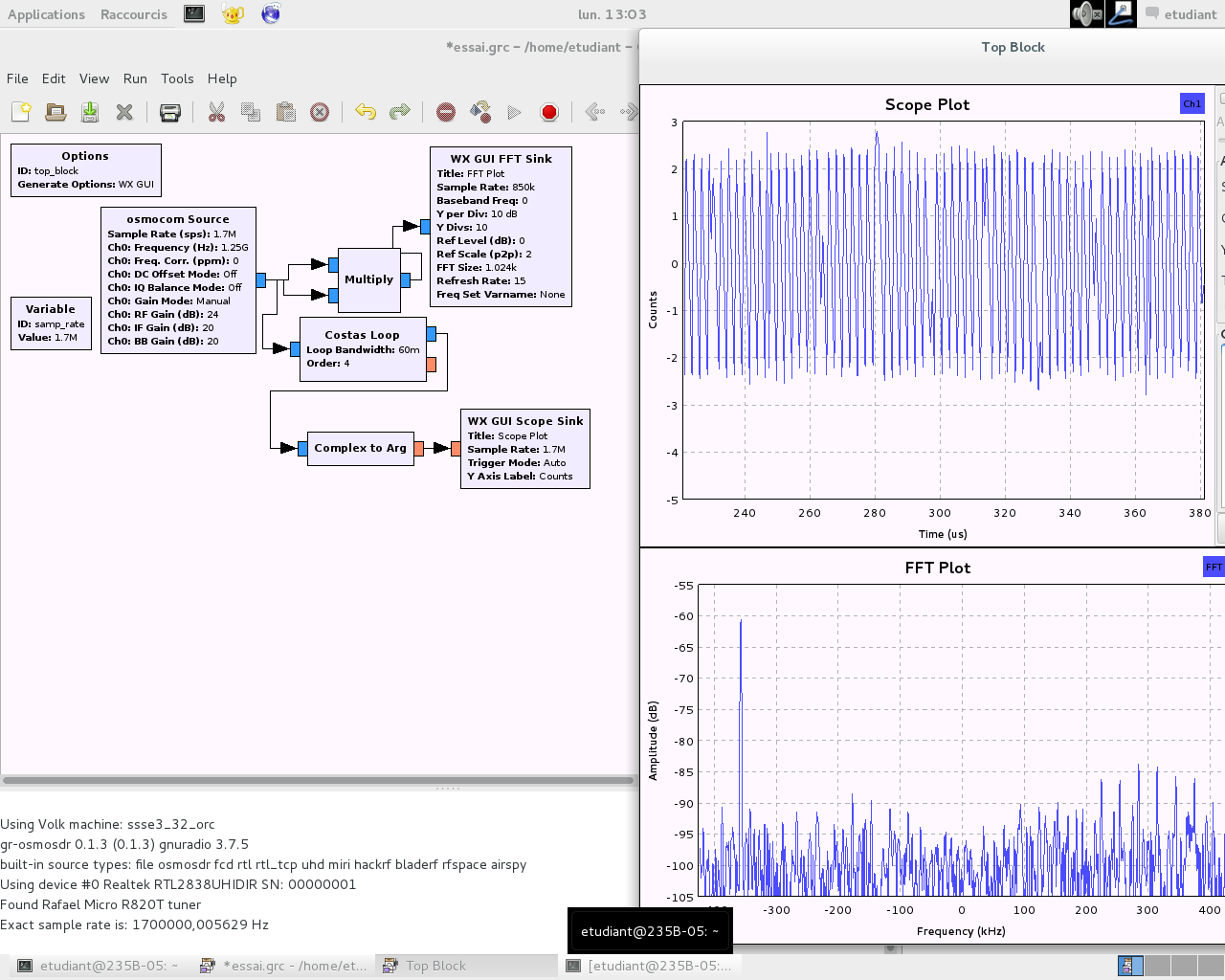
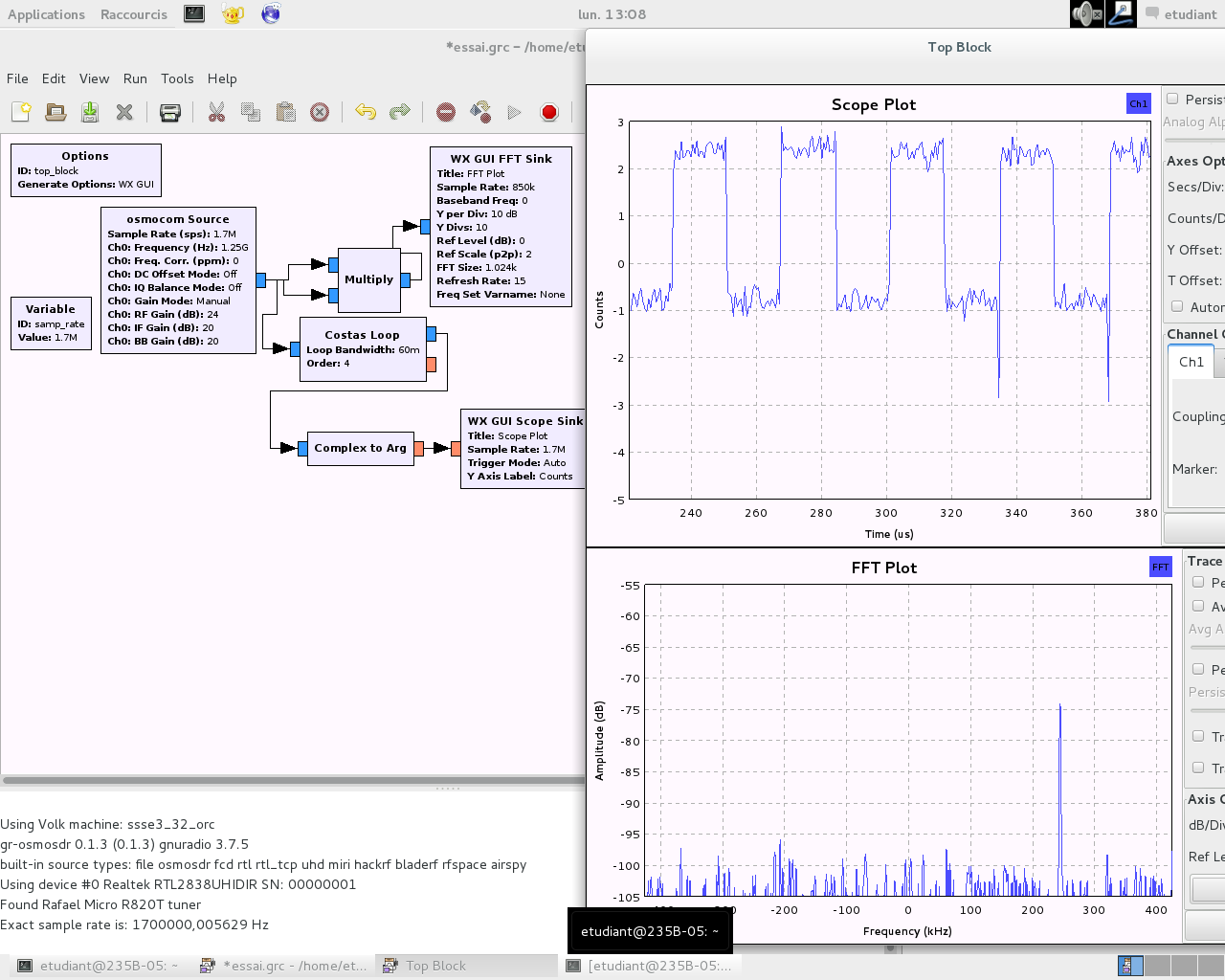
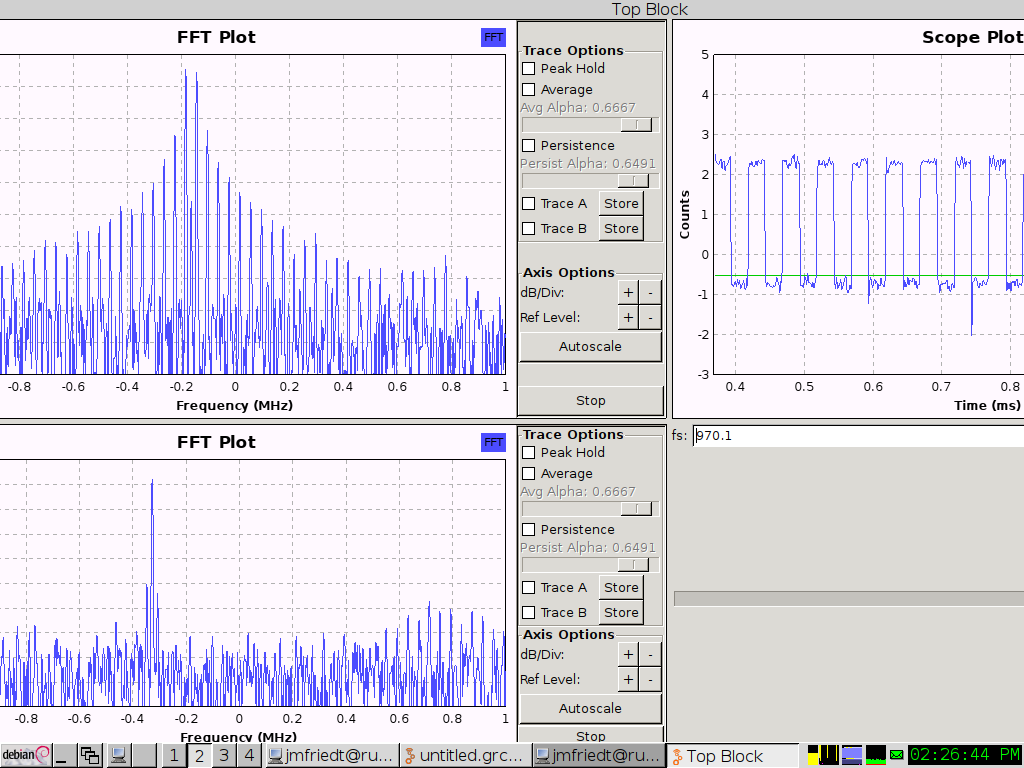
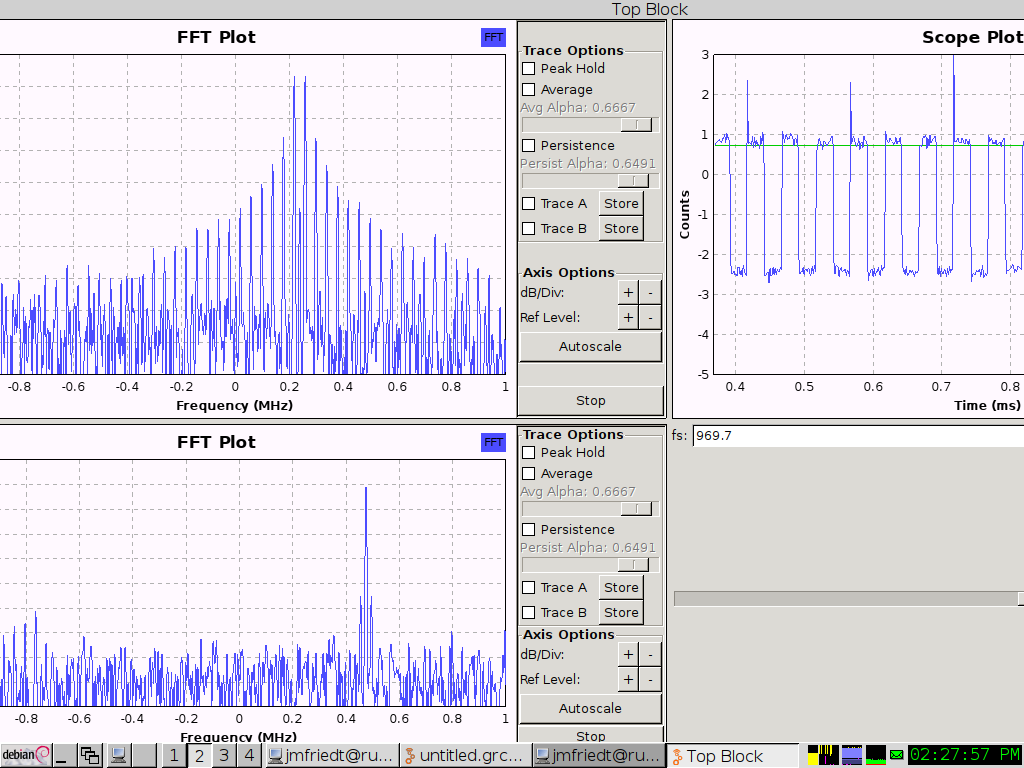
1. Demonstrate the ability to demodulate the phase-modulated signal being transmitted (Fig. 17). What is the maximum offset acceptable between LO and the carrier for the feedback control loop to lock ?

FSK modulation

Amongst the classical modulation schemes, FSK encodes two possible bit states as two frequency modulations of the carrier. On the receiver side, a FM demodulator returns two voltages for the two possible states of the bit stream (Fig. 19).

1. What happens when the local oscillator and the emitter oscillator are offset ? How does a modulation over the carrier correct this issue ?

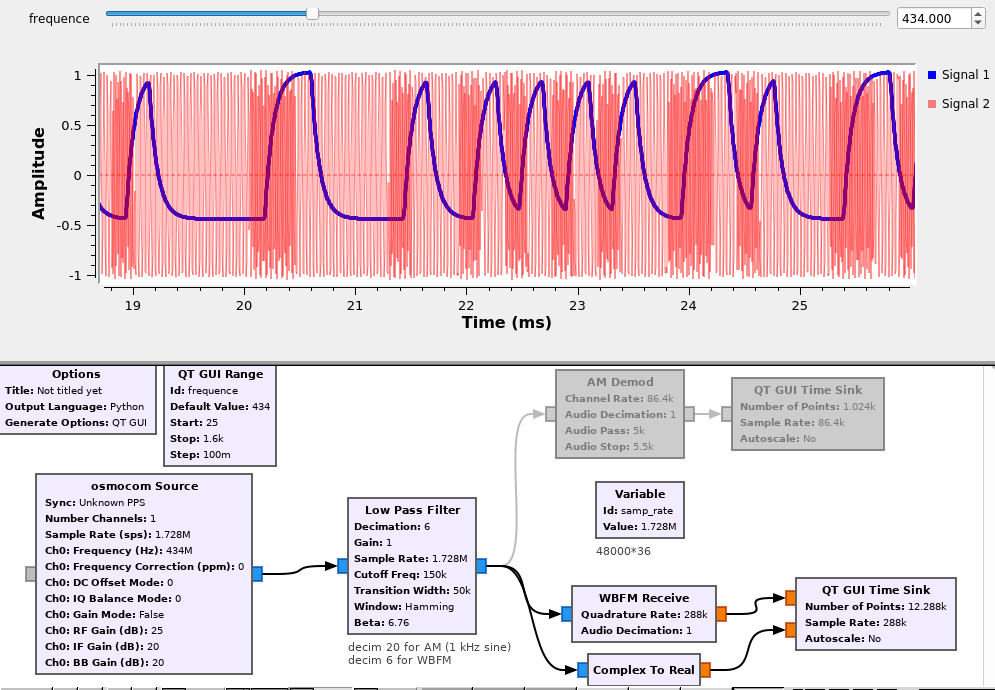
1. Considering that the signal controlling the VCO is generated by a RS232-compatible UART from a microcontroller, what is the baudrate of the digital communication shown in Fig. 19 ?

Connecting to an external sentence decoding tool

A simple approach to analyze sentences from demodulated signal is to use an external tool called multimon and its latest revision multimon-ng. All decoders are eliminated (-c) and graphical output as well as POCSAG messages transmitted at 1200 bauds are displayed with multimon-ng -t raw -c -a POCSAG1200 -a SCOPE myfile. Using the raw interface type assumes that signed 16-bit data are streamed at 22050 Hz.

We focus on signals emitted in France by pagers, also known at the time by their brand name Tam-tam or Tatoo and still used by the e*message company ¹. The communication protocol is called, and is briefly described at http://fr.wikipedia.org/wiki/POCSAG. We learn that in France, the six allocated frequencies are 466.{025;05;075;175;20265;23125} MHz.

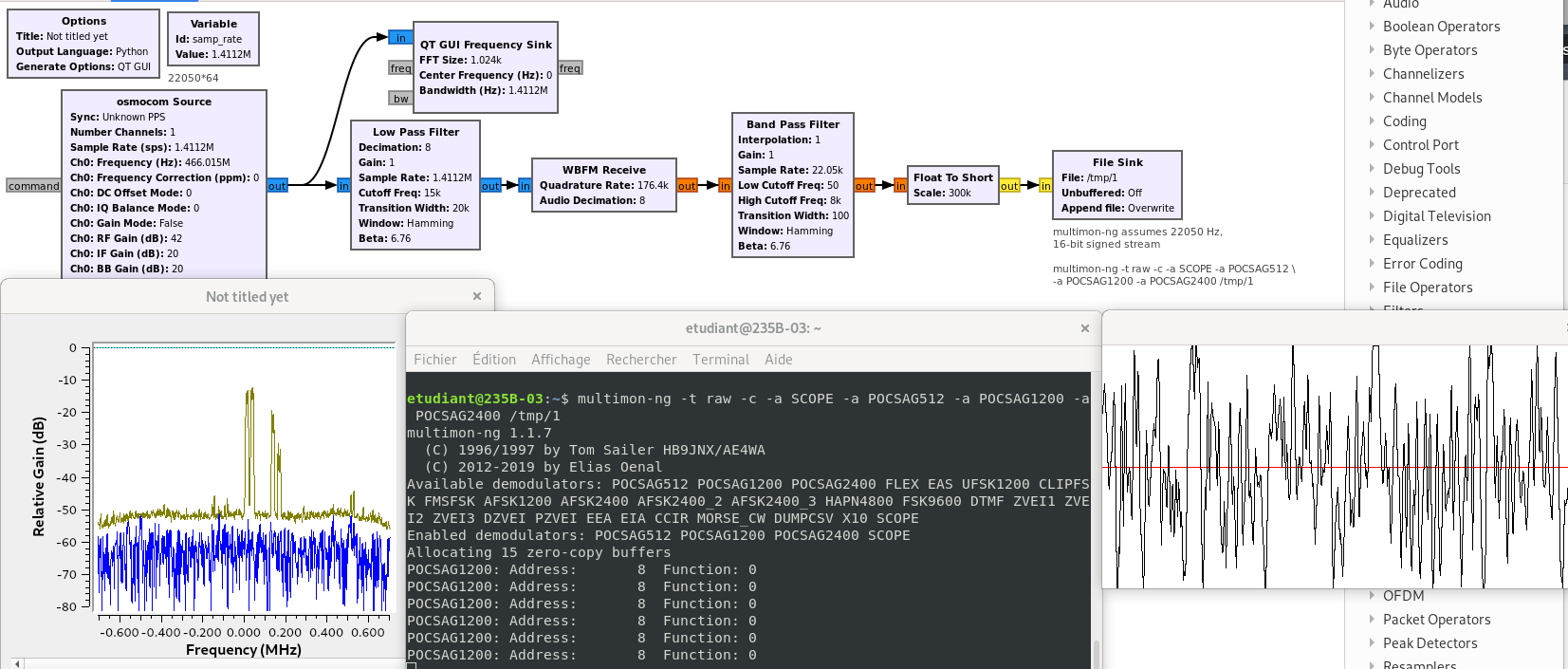
multimon-ng ² handles a wide variety of modulation schemes dating back to the time when receiving radio signal was done using a dedicated receiver whose audio output was actually connected to the sound card input of the personal computer. Today, this link has become virtual through a named pipe (mkfifo unix command).

A stream through a named pipe only starts flowing when both ends of the pipe are connected. Launching the gnuradio software is not enough to run the acquisition, and the processing only starts after running multimon.

The other configuration subtlety lies in complying with the expected data rate for multimon-ng to handle the data stream, namely a rate of 22050 Hz with 16 bit integers.

• Create a named pipe with mkfifo mypipe

• Create a data sink in GNURadio-companion meeting the data format requirements

• Connect multimon to the named pipe with multimon -t raw mypipe

1. Watch the result (Fig. 20)

Notice the high-pass filter at the output of the frequency demodulator and the floating point to integer converter. Indeed, any frequency offset between the emitter and FM receiver oscillators will yield after the demodulation to an constant voltage offset. Le high pass filter not only remove this offset but also decimates the data stream to reach the datarate expected by multimon.

Multichannel analysis

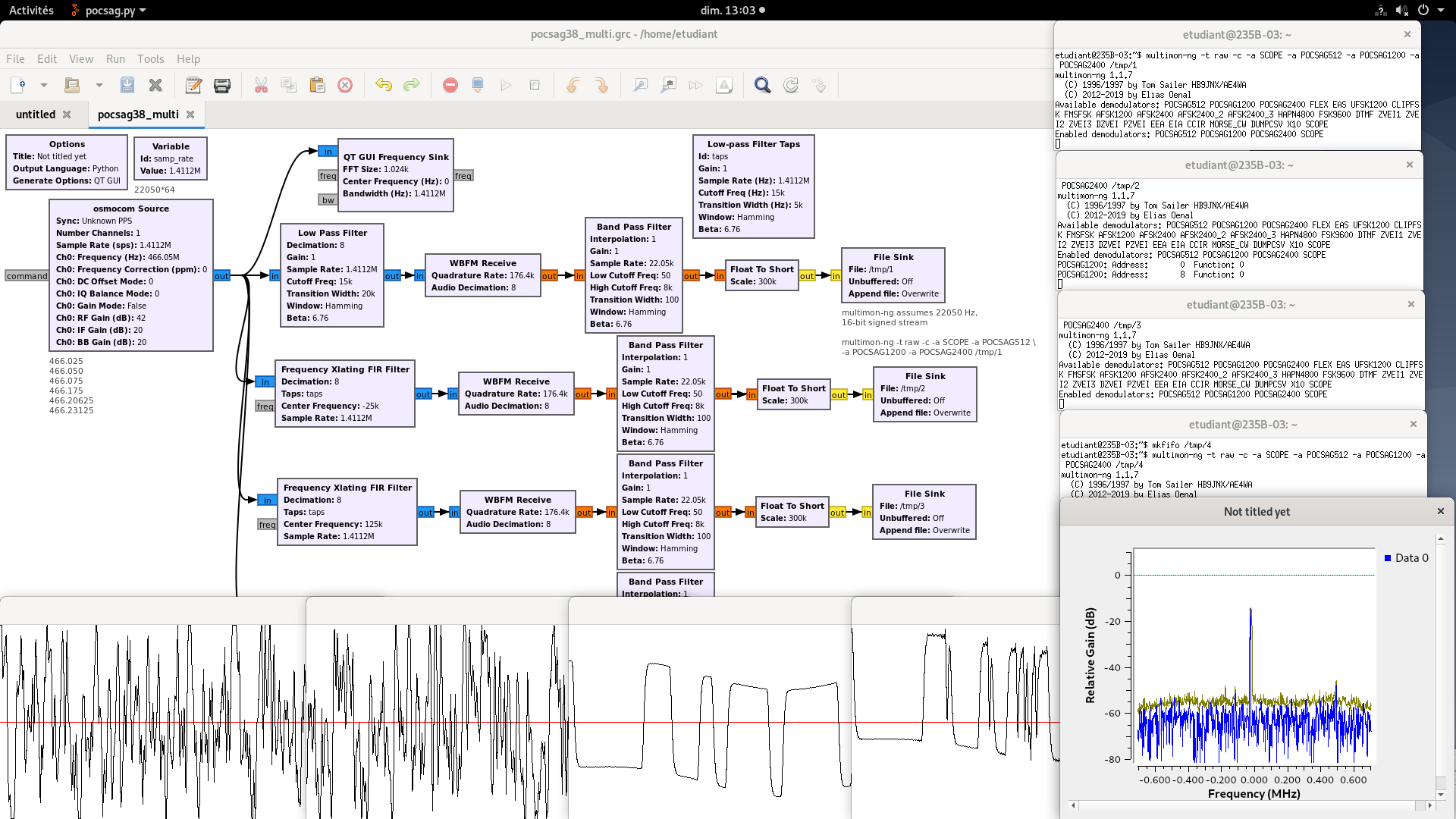
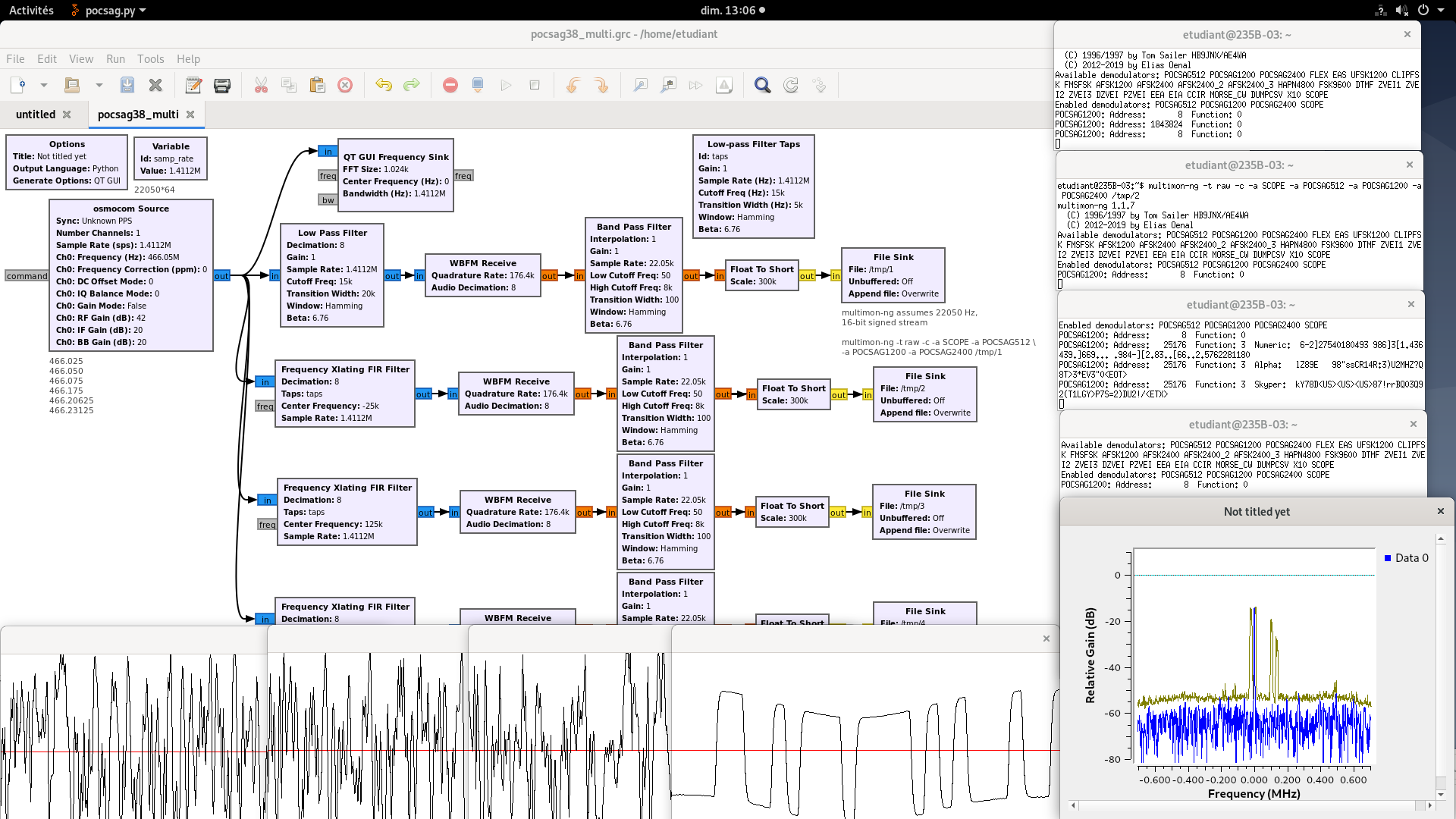
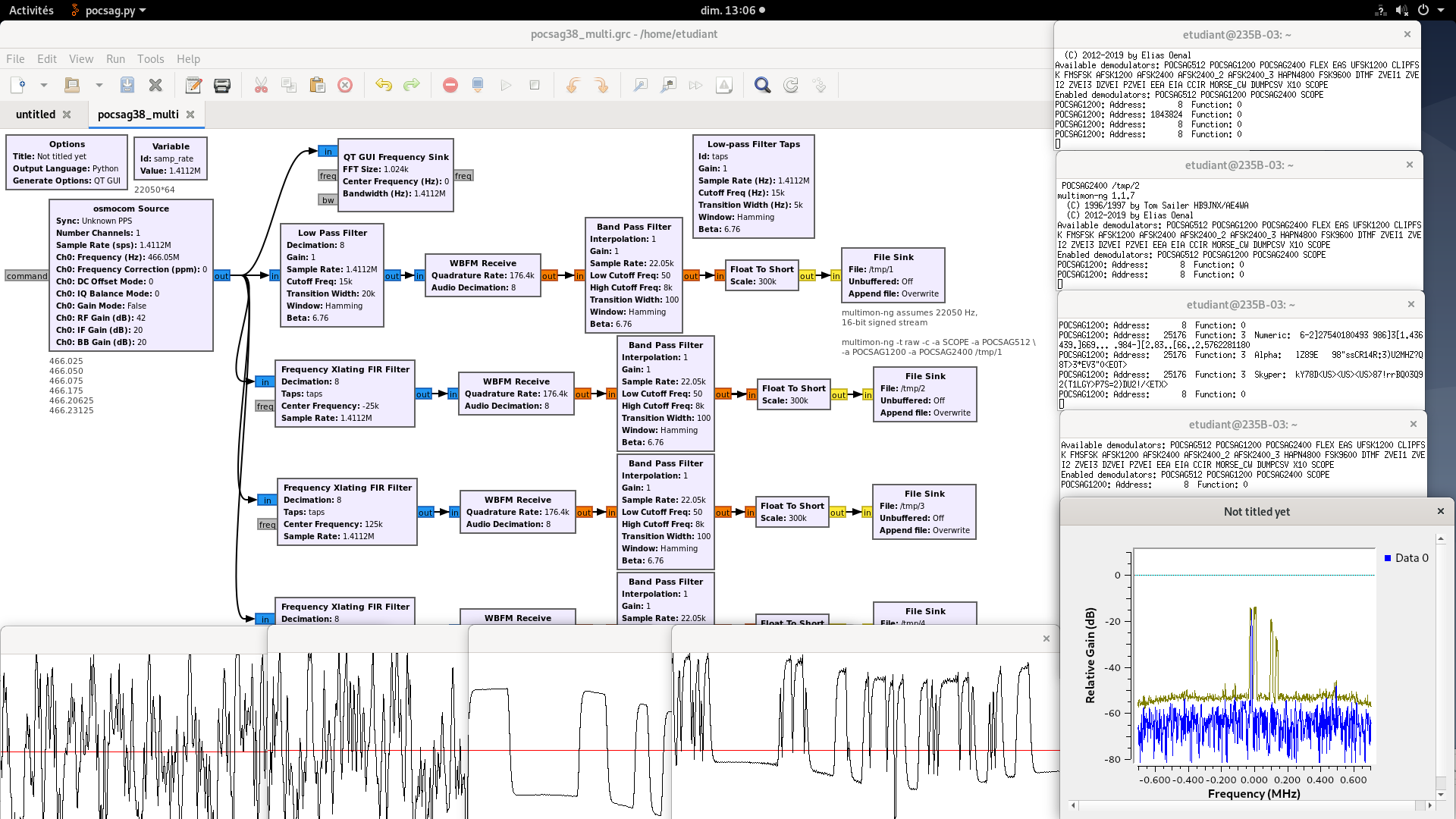
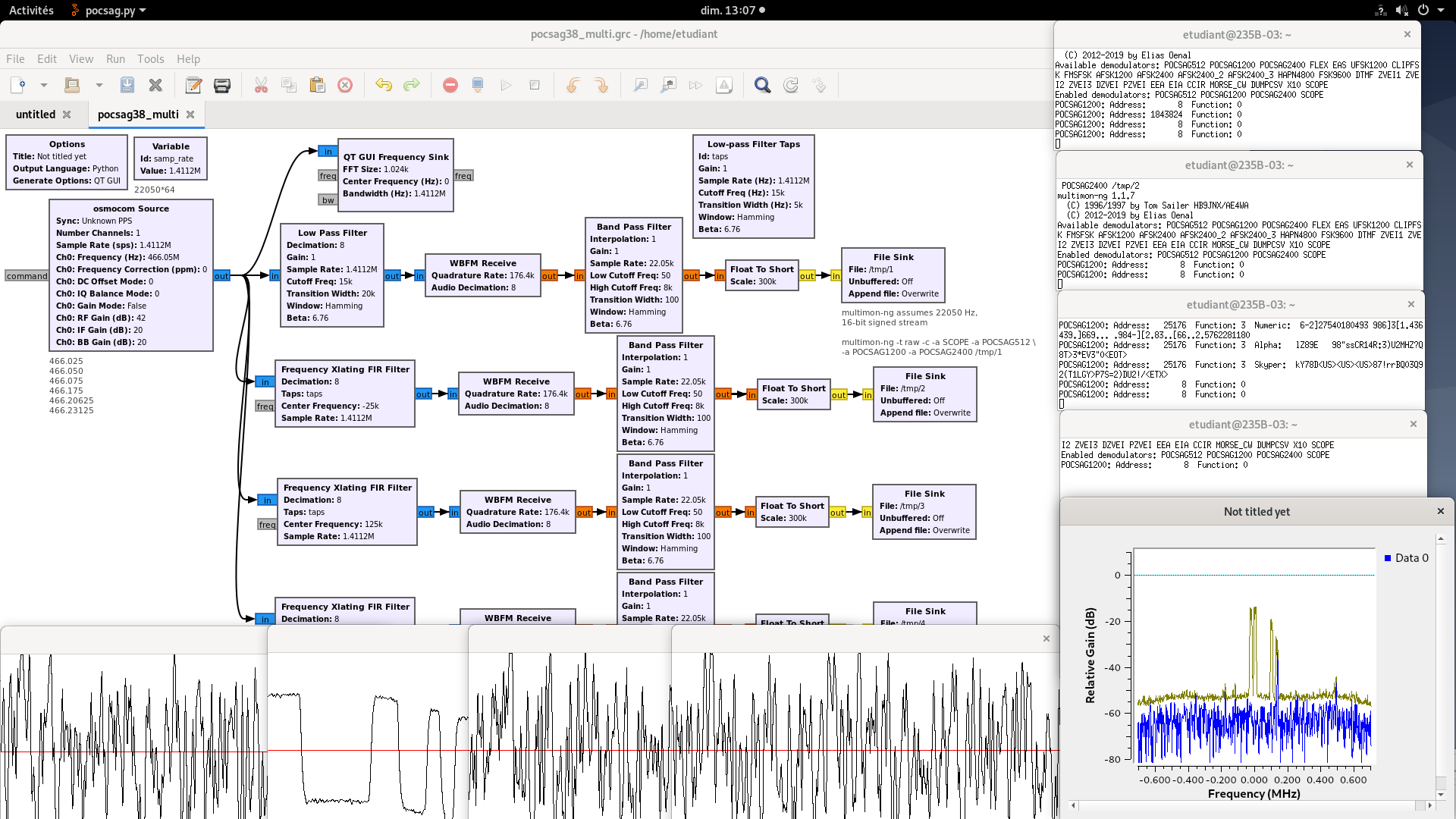
POCSAG is characterized by several radiofrequency channels. So far we have only decoded a single channel by selecting its carrier frequency. We now wish, since the I/Q stream provides all the information carried by all the channels, to decode the content of all communication channels in parallel (Fig. 24).

From a signal processing perspective, we must band-pass each channel and process the associated information, without being polluted by the spectral content of adjacent channels. Practically, we frequency shift each channel close to baseband (zero-frequency), and introduce a low-pass filter to cancel other spectral contributions.

This processing scheme is so classical that it is implemented as a single GNURadio Companion bloc: the Frequency Xlating FIR Filter. This bloc includes the local oscillator with which the frequency must be shifted by mixing, and the low-pass filter. A low-pass filter is defined by its spectral characteristics: the FIR coefficients are obtained with
firdes.low_pass(1,samp_rate,15000,5000,firdes.WIN_HAMMING,6.76). This command is located in a variable whose name is used for fill the characteristics of the filter, called taps.

Alternatively, in this example with have used the Low-pass Filter Taps block for generating the taps defining the Xlating FIR filtering transfer function.

1. Demodulate two POCSAG channels simultaneously.

This processing strategy can be extended to any number of channels, as long as processing power is available. Practically, we have observed that it is unwise to process more channels than computer cores available on the processor.

Furthermore, this conclusion can be extended to any number or kind of modulation schemes transmitted within the analyzed bandpass, as will be shown next with the broadcast FM band.

Radio Data System (RDS)

In the case of the broadcast FM band, the two mono (left+right) and stereo (left-right) channels are located around the 19 kHz pilot signal of the radiofrequency carrier, and on the other hand the digital stream of the emitter (RDS) is located 57 kHz from the baseband. These two information are independently demodulated since all the information needed have been gathered within the FM station demodulation of the output of the WBFM block is provided at a rate of more than 115 ksamples/s .

1. Analyze Fig. 28 and observe the two demodulation paths, analog audio on the one hand and digital on the other.

The RDS information is a digital BPSK modulation at 1187.5 bps. The Costas loop takes care of identifying the carrier offset and compensating for the frequency offset to provide a copy of the emitted carrier, but does not solve the issue of selecting the sampling time. Various bitstream synchronization blocks are available in GNU Radio: here we use Mueller and Müller (M&M) clock recovery block with complex input, which implements a discrete-time error-tracking synchronizer. Indeed at the output of the MM Clock recovery block, the two phase states are clearly separated and stable. The Omega parameter of the MM Clock recovery block is the initial estimate of the number of samples the bits and should be as low as possible, above 2. The efficiency of the clock recovery block is dependent on the preliminary filtering designed to avoid intersymbol mixing: the Root Raised Cosine filter provides much better results that the basic low-pass filter. Bottom left of each bottom chart of Fig. 28, the phase output of the Costas loop clearly shows the two possible bit states with no linear drift as would be observed with a leftover frequency offset.

9 Introduction to GNURadio: http://jmfriedt.free.fr/en_sdr.pdf (2012) RDS decoding: http://jmfriedt.free.fr/lm_rds_eng.pdf (2017)

Answers

1. the API is described at http://gnuradio.org/doc/doxygen/classgr_1_1filter_1_1fir__filter__fff.html and shows that the filter is defined with

   self.band_pass_filter_0.set_taps(firdes.band_pass(1, self.samp_rate, self.f-self.b, self.f+self.b, \
        self.b/5, firdes.WIN_HAMMING, 6.76))

2. after

           # Connections
           ##################################################
           self.connect((self.analog_noise_source_x_0, 0), (self.blocks_throttle_0, 0))
           self.connect((self.band_pass_filter_0, 0), (self.qtgui_freq_sink_x_0, 0))
           self.connect((self.blocks_throttle_0, 0), (self.band_pass_filter_0, 0))

   we add

           print(len(self.band_pass_filter_0.taps()))

3. selecting a sampling rate compatible with the sound card sampling rate will output the signal on the headphone output.

4. Replacing the frequency sink with a time sink (oscilloscope) and replacing the audio output with a throttle block yields:
   

5. the number of taps is not dependent on the center frequency but only on the transition width (or more accurately, on the ratio of the sampling rate to the transition width). Adding print(len(self.fir_filter_xxx_0.taps())) as was done earlier shows that

   Sampling rate	Center frequency	Transition width	Number of coefficients
   96000	14000	100	6545
   48000	14000	100	3273
   48000	14000	50	6545
   48000	7000	50	6545
   96000	7000	100	6545

   demonstrating that the number of coefficients (tap length) is independent on center frequency and only dependent on the ratio of the sampling frequency to the transition width.

7. The answer to the last two questions is
   

8. Aliasing will bring the 95560=96000-440 back to baseband at 440 Hz: no difference will be heard with the initial flowchart.

9. The FM broadcast band is located around 100 MHz or a 3-m wavelength, so the optimal dipole length is 1.5 m or a monopole over a ground plane 75 cm long (quarter-wavelength).

10. The FM broadcast band emits two audio channels (stereo sound) and the digital Radio Data System (RDS) centered around 57 kHz from the carrier. Spacing between FM channels is 200 kHz, well within the $2\times 57$ kHz needed to broadcast all information. Hence, a 100-kHz low-pass filter (or a bandwidth of $2\times 100$=200 kHz) will reject adjacent channels and still propagate all information from the received channel.

11. The broader the sampling rate, the more FM broadcast channels can be visible at a given time, but the more processing power is needed to sink higher datarates.

12. aU means audio Underflow (too few samples) and aO means audio Overflow. If the datarates between radiofrequency signal collection and audio signal emission are inconsistent, these messages will continuously flow in the terminal.

13. see Fig. 6

14. The frequency synthetisizer generates either 400 Hz or 1 kHz AM or FM modulated signals.

15. Squaring the BPSK signal will shift the squared signal frequency offset to twice the offset value, and this doubled frequency offset must remain within the sampling band of the receiver.

16. DC offset since the FM demodulator acts as a frequency to voltage converter. Adding a modulation, e.g. AFSK (Audio Frequency Shift Keying) on NOAA satellites, cancels this offset.

17. 0.4 ms peak-to-peak period, i.e. for transmitting two symbols (0 and 1) so 1000/0.4=2500 which is most certainly a 2400 baud transmission for two symbols, or 4800 bauds which is indeed the configuration of the XE1203 we used.

18. see Fig. 20

19. see Fig. 24

20. see Fig. 28